| Страница: 1 2 3 4 5 6 7 8 9 10 |
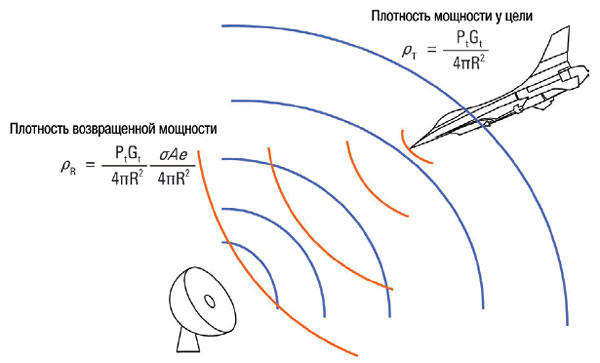
Рисунок 3 – Переданная и отраженная мощность, возвращенная к радиолокатору
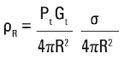
где; ρR – плотность возвращенной к радиолокатору мощности в ваттах на квадратный метр;
σ – ПСР в квадратных метрах.
Часть этого сигнала, отраженного целью, будет перехватываться антенной радиолокатора. Мощность этого сигнала будет равна плотности возвращенной мощности у антенны, умноженной на эффективную площадь антенны Ае.
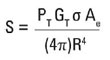
где: S – мощность сигнала, принятого приемником, в ваттах;
PT – переданная мощность в ваттах;
GT – усиление передающей антенны (отношение);
σ – ПСР в квадратных метрах;
R – радиус или расстояние до цели в метрах;
Ae – эффективная площадь приемной антенны в квадратных метрах.
Теория антенн позволяет нам выразить усиление антенны через её эффективную площадь в виде:

где:
GR – усиление приемной антенны;
λ – длина волны сигнала радиолокатора в метрах.
Выражение для мощности принятого сигнала теперь может быть упрощено. Заметьте, что для моностатического радиолокатора усиление антенны GT и GR являются эквивалентными. Предположим, что у нас есть случай для такого преобразования.
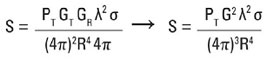
где: S – мощность сигнала, принятого приемником, в ваттах;
PT – переданная мощность в ваттах;
G – усиление антенны (предположим одну антенну для приема и передачи);
λ – длина волны сигнала радиолокатора в метрах.
σ – ПСР цели в квадратных метрах;
R – радиус или расстояние до цели в метрах.
Теперь, когда мощность сигнала у приемника известна, следующим шагом будет анализ того, как приемник будет обрабатывать сигнал и извлекать из него информацию. Основным фактором, ограничивающим приемник, является шум и результирующее отношение сигнала к шуму (S/N).
Мощность шума (теоретический предел) на входе приемника, описываемого как шум Джонсона или тепловой шум, является результатом случайного движения электронов и пропорционален температуре.
N = kTBn,
где:
N – мощность шума в ваттах;
k – постоянная Больцмана (1,38 x 10-23) джоулей / градус Кельвина;
Т – температура в градусах Кельвина;
Bn – шумовая полоса системы.
При комнатной температуре 290°К имеющаяся на входе приемника мощность шума будет равна 4 x10–21 Вт/Гц, что соответствует –203,98 дБВатт/Гц или –173,98 дБм / Гц. Имеющаяся на выходе приемника мощность шума всегда будет больше, чем предсказывает приведенное выше уравнение, из-за шума, генерируемого внутри приемника. Шум на выходе будет равен идеальной мощности шума умноженной на коэффициент шума и усиление приемника.
No = GFnkTB,
где:
No – общий шум приемника;
G – усиление приемника;
Fo – коэффициент шума.
Кроме коэффициента шума, другие ограничивающие факторы включают шумы генератора (такие как фазовый шум или амплитудный шум), паразитное излучение, остаточные сигналы или сигналы зеркальной боковой полосы частот. Эти сигналы могут или не могут быть подобными шуму, но они будут влиять на способность обрабатывать принятые сигналы. Для простоты эти факторы не будут конкретно рассматриваться при выводе формулы. Однако фазовый шум и паразитное излучение являются важными для радиолокации измерениями, которые могут влиять на характеристики радиолокатора, и поэтому включены как часть последующего обсуждения в эти заметки по применению.
Как справедливо замечено, имеющаяся на выходе приемника мощность шума всегда будет больше, чем тепловой шум Джонсона. Это происходит из-за дополнительного шума, который генерируется внутри приемника. Общий шум на выходе будет равен мощности шума Джонсона, умноженной на коэффициент шума Fo и усиление приемника G.
Усиление приемника может быть переписано как отношение сигнала на выходе приемника к сигналу на входе (G = So/Si). Решая уравнение для коэффициента шума, получим:
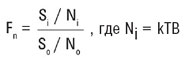
По определению, коэффициент шума является отношением сигнал/шум на входе к сигнал/шум на выходе.
Уравнение может быть переписано в другой форме:
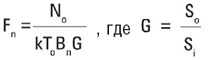
где:
Fn – коэффициент шума ;
No – общий шум приемника;
G – усиление приемника;
So – сигнал на выходе приемника;
Si – сигнал на входе приемника;
To – омнатная температура;
k – постоянная Больцмана;
Bn – шумовая полоса приемника.
Так как коэффициент шума описывает ухудшение отношения сигнал/шум, когда сигнал проходит через систему, то может быть определен минимальный обнаруживаемый сигнал (МОС) на входе, который соответствует минимальному отношению сигнал/шум на выходе при мощности шума на входе равной кТВ.
Si → Sminкогда условие минимума So/No определено выражением:
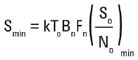
где:
Smin – минимальная мощность, требуемая на входе приемника;
Fn – коэффициент шума;
(So/No)min – минимальная величина отношения, требуемая для обнаружения сигнала процессором приемника.
Теперь, когда минимальный уровень сигнала, требуемый для превышения шума системы, определен, максимальная дальность действия радиолокатора может быть вычислена путем приравнивания МОС(Smin) к уровню сигнала, отраженного от нашей цели на максимальной дальности (установкой Smin равной выражению для S выше).
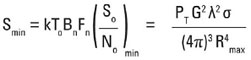
Из этого уравнения мы можем выразить максимальную дальность действия нашего радиолокатора
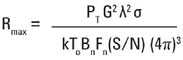
где:
Rmax – максимальное расстояние до обнаруживаемой цели в метрах;
PT – передаваемая мощность в ваттах;
G – усиление антенны (предположим одну антенну для приема и передачи);
λ – длина волны сигнала радиолокатора в метрах.
σ – ПСР цели в квадратных метрах;
k – постоянная Больцмана;
To – комнатная температура в градусах Кельвина;
Bn – шумовая полоса приемника в герцах;
Fn – коэффициент шума;
(S/N) – минимальная величина отношения, требуемая для обнаружения сигнала процессором приемника.
Это уравнение описывает максимальную дальность цели для нашего радиолокатора, основанную на передаваемой мощности, усилении антенны, ПСР со стороны цели, коэффициенте шума системы и минимальном отношении сигнал/шум. На самом деле оно является упрощенной моделью характеристик радиолокатора. Имеются много факторов, которые также будут затрагивать характеристики системы, в том числе изменения в предположениях, сделанных при выводе этого уравнения. Двумя дополнительными факторами, которые должны быть учтены, являются потери в системе и интегрирование импульса, которое может возникнуть при обработке сигнала. Потери в системе могут произойти как на пути передачи, так и на пути приема. В случае классического применения импульсного радиолокатора можно предположить, что от данной цели будет принято множество импульсов для каждого положения антенны радиолокатора (так как полоса пропускания антенны больше нуля, очевидно, что радиолокатор будет останавливаться на каждой цели некоторое временя), поэтому их можно проинтегрировать для улучшения характеристик радиолокационной системы. Так как наше интегрирование не может быть идеальным, мы будем использовать термин эффективность интегрирования Ei(n), основанный на числе интегрированных импульсов, для описания улучшения от интегрирования.
Включение этих терминов в уравнение радиолокатора дает в результате выражение:
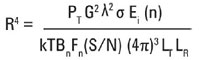
где:
LT – потери на пути передачи;
LR – потери на пути приема;
Ei(n) – коэффициент эффективности интегрирования.
Все уравнение может быть преобразовано в логарифмическую форму (дБ) для упрощения обсуждения:
где:
R – максимальное расстояние в метрах;
PT – передаваемая мощность в ваттах;
G – усиление антенны в дБ;
λ – длина волны сигнала радиолокатора в метрах.
σ – ПСР цели, измеренная в дБсм или в дБ относительно квадратного метра;
FN – величина шума (величина шума равна коэффициенту шума, преобразованному в дБ);
S/N – минимальное отношение сигнал / шум, требуемое функциям обработки приемника для обнаружения сигнала в дБ.
Член 33 дБ образуется из 10 log(4Π)3 , а член 204 дБВатт/Гц из шума Джонсона при комнатной температуре.
Логарифмическое значение для ПСР σ dBsm определяется в дБсм или в дБ относительно одного метра сферы (с поперечным сечением в один квадратный метр), которая является стандартной целью для измерений поперечного сечения радиолокатора.
| Страница: 1 2 3 4 5 6 7 8 9 10 |

